18、置换密码(栅栏密码,列置换密码,多步置换,乘积密码,转轮机)其中注意转轮机每输入一个字母快速转子就会转动一格
栅栏密码
将明文字母以对角线的方式写入,再逐行读出密文字母。
例子:

列置换密码
明文以矩形方式一行行写入,但一列列的读出,密钥是矩形的长度和列读出顺序。
例子:

多步置换密码
多次进行列置换密码操作,这样难以反向重构。
例子:

乘积密码
由于语言的统计特征,单纯使用代替或者置换是不够的。
连续多次使用密码使得算法更安全:两次代替得到更为复杂的代替密码,两次置换
到更为复杂的置换密码,一次代替加一次置换得到安全性高得多的密码。
是从古典密码过渡到现代密码的桥梁。
转轮机
每个转子对应一个代替密码;
每个转子产生一个对应着26个密文字母表的多表代替密码(维吉尼亚密码);
每次按键后,转子旋转一个刻度;
每个转子的输出是下一个转子的输入;
在每个转子循环完一个周期后,相邻的下一个转子旋转一个刻度。
(一个3-转子转轮机产生26^3个密文表)
19、对公钥密码的一些误解
公钥密码比对称密码更安全
公钥密码的出现使得对称密码变得过时
与对称密码使用KDC繁琐的握手方式分配密钥相比,公钥密码的密钥分配容易。
20、公钥密码的要求
用公钥加密的信息可以用私钥解密恢复(基本条件) D(E(M,PU),PR)=M
给定加密密钥,想得到解密密钥从计算上不可行(安全条件)
当相关的加密密钥已知,做相应加密操作是快速高效的(工程使用条件)
加密的顺序可以互换(可选条件)D(E(M,PU),PR)=D(E(M,PR),PU)=M
21、对称密码与公钥密码的对比 分析
公钥密码
使用两个密钥(公钥和私钥)
PU的公开不会泄露PR
由于通信不对称,加密信息的人不能解密信息
基于数学函数而不是代替和置换
对称密钥(秘密钥):
使用一个密钥,双方共享
密钥泄露导致通信的安全性被破坏
由于通信对称,双方地位平等,因此不能防止发送者否认发送,也不能防止接收者伪造信息并声明是发送者发送的。
22、公钥密码体制的几张图以及相关的安全属性
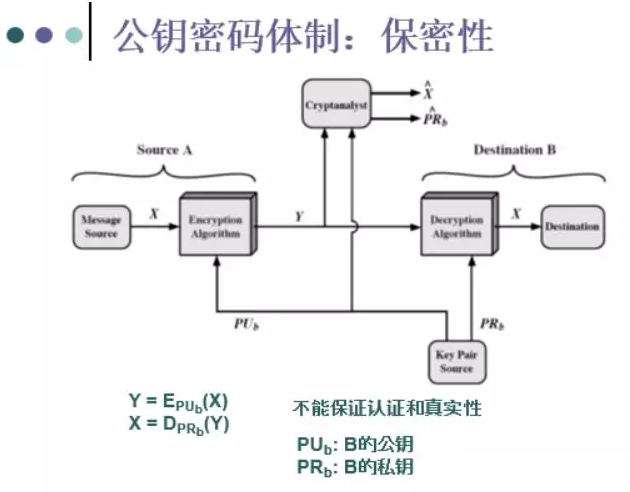

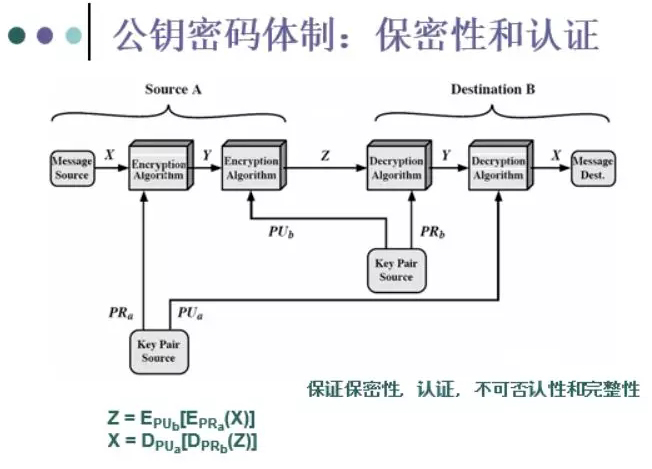
加解密——保密性
数字签名——认证、完整性和不可否认性
密钥交换——提供会话密钥
23、单向函数与单向陷门函数
单项函数:每个函数值都存在唯一的逆,并且计算函数值是容易的,但求逆却是不可行的。
单向陷门函数:一个函数,若计算函数值很容易,并且在缺少一些附加信息时计算函数的逆是不可行的,但是已知这些附加信息时,可以在多项式时间内计算出函数的逆。
24、公钥密码分析
针对PR的穷举攻击
数学分析攻击:从PU中视图推出PR
穷举消息攻击
25、哈希函数的定义及六种基本使用模式
hash函数H将可边长的数据块M作为输入,产生固定长度的Hash值h=H(M)。


26、抗强碰撞性,抗弱碰撞性
单向性:给定h,反向求出x,使得H(x)=h不可行
抗弱碰撞性:给定x,找到y,使得H(x)=H(y)不可行
抗强碰撞性:找到任意的x,y使得H(x)=H(y)不可行
27、哈希函数的通用结构(迭代压缩函数)
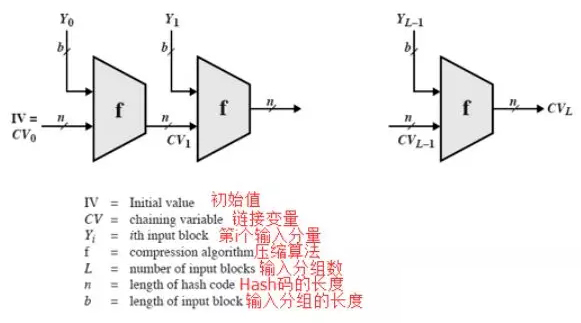
如果每个f是抗碰撞的,则哈希结果也是抗碰撞的。
28、数字签名包含的属性及定义
签名的属性:
防止发送方抵赖,包括签名内容、时间(不可否认性)
除了发送方,其他人不能伪造签名和被签名内容(真实性,完整性)
可被第三方验证以解决争端(可仲裁性)
定义:数字签名是一种认证机制,是消息产生者在消息后附加的一个签名码。 可以保证消息来源的真实性/不可否认性、完整性。
数字签名的属性:
必须依赖被签名信息——确保完整性
必须使用发送者独一无二的信息(PR)——防止伪造和否认(真实性/不可否认性)
相对容易产生
相对容易验证(PU)
计算上不能被伪造(对于给定数字签名伪造新消息与之对应、对于给定消息伪造数字签名与之对应)
存储数字签名的拷贝是可行的
29、哈希函数在数字签名中的用处
减少数字签名和通信的长度
维护消息和签名的对应关系以防伪造(真实性、完整性)
30、仲裁数字签名

(责任编辑:安博涛)





