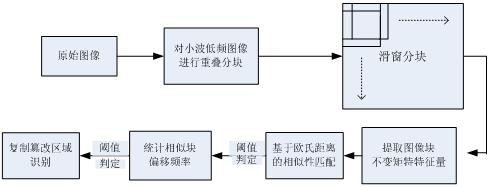
详细描述如下：
    （1）设 I_{M x N}  为待检测的灰度图像，其中M x N 为图像的大小； 
    （2）对图像进行j级小波变换，变换后的小波低频图像为A_{m x n}，其中 ，  ，  为下取整操作；

 
图1 检测算法流程图

    （3）设定窗口块W的大小为a X b（这里假设设定分块的大小小于要检测的复制图像区域的大小），对小波低频图像进行一次移动一个像素的滑动，则共有N_W =(m-a+1) X (n-b+1) 个块； 
    （4）对每个图像块进行不变矩特征提取，则特征空间由a X b维下降到了7维。对得到的特征向量按行进行字典排序，得到排序后的N_W X 7维的特征矩阵B； 
    （5）把式（7）与预设阈值  相比较，即可得多组相似度很高的图像块。计算它们对应的图像块的坐标值的偏移矢量  ； 
    （6）对满足  或者 的  ，统计其偏移频率  ，得到偏移频率矩阵C（初始化为零）：  =  +1； 
    （7）对得到偏移频率矩阵C进行大于阈值T判断，判别出图像中是否存在复制图像区域。如果存在，进入下一步；如果没有，则算法结束； 
    （8）对偏移频率大于阈值T的那些偏移矢量对应的图像块位进行标识，如果这些具有相同偏移矢量的块是相连的，则组成了图像复制粘贴的区域，如果标识块是相互不相连或相连小的，则可能是噪声，可通过数字形态学中的膨胀、腐蚀操作进行去除。 
    在图像Copy-move篡改的检测中，利用不变矩^[7] 作为特征检测此类篡改检测，已经被证实是一个很好的方法。而基于小波和不变矩来检测不但可以保证对于经过一般几何变换的篡改有很好的检测效果，而且有效减少算法的计算量，提高检测速度。

3 试验比较 

    将本文算法与文献 ^[1,2,7]进行比较，以一大小为512 X 512 X24(bit)图像为例。先把彩色图像转换为灰度图像进行处理，设定分块大小为8*8(bit)，对每个图像块分别进行特征提取进行排序，它的 
                                                                                           表1   本文算法与文献算法的比较结果 
                                                                                    图像特征描述     8*8图像块的数目               特征维数 
                                                          Fridrich算法     DCT&量化       （512-8+1)² =255,025             64
 
                                                          Popescu算法        PCA            （512-8+1)² =255,025             32
                                                          基于不变矩算法    不变矩         （512-8+1)² =255,025              7
                                                          本文提出的算法 DWT&不变矩 (256-8+1)²=62,001                 7
  
行数目即代表了分块的数目，列数代表图像块特征维数。表1列出了四种算法的比较结果，本文算法的图像块数目大约是其余三种算法的1/4，本文算法中图像块的特征维数是7维，而Fridrich和Popescu算法中图像块的特征维数分别是64维和32维，显然比本文的算法中提取的特征维数多了很多。通过表1可以显而易见的辨识出本文算法的效率优势。在相同的实验条件下，本文算法从缩小图像块数目和降低特征空间维数两方面更好地提高了检测效率。

(责任编辑：adminadmin2008)