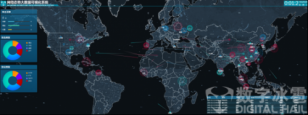
接着，他们对最后计算得到的整合图中的边进行了处理。为了更好的描述边的分布和图的拓扑结构，他们对图中的边进行了层次聚类；接着采用贝赛尔曲线表示这些边，并采用滚雪球的方法对边进行可视化(图7)。

 

图7 左图，直接用直线展示边的布局；右图，对边进行一系列处理后的布局

最后，他们采用Welsh-Powell方法对图中的顶点进行着色。因为同个顶点的位置分布可能因为一些异常值，导致在空间上不能聚集在一起。为了帮助用户快速的识别同个顶点的位置分布，他们对图中的顶点进行了聚类处理。针对每个聚类，他们计算了群簇的边缘，并将表示同个顶点的群簇通过图8的方法，连接起来。

 

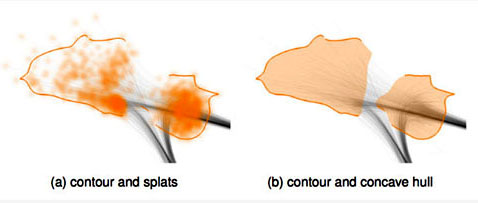
图8 对顶点进行聚类，添加边缘的结果

根据轮廓之间的空缺方向，用户可以将属于同个顶点的群簇链接起来。

接下来，我将介绍两个实例，验证这个方法的可用性。

第一个例子使用的是人造数据。在这个数据中，有五个顶点，8条边。每条边的概率分布如图9(c)第一行所示。图9(a)表示的是这个人造数据的期望图。我们可以发现，这个布局可以清晰的展示图的拓扑结构，但不能将边的不确定信息展示出来；图9(b)表示的是通过文章的方法计算得到的布局。

它清晰的展现了图的拓扑结构和顶点的位置分布；图9(c)表示的是边的统计信息。每一列表示一条边，第一行表示边存在与否的概率分布，第二行表示采样获得的边的概率分布，第三行表示边的欧拉距离分布。我们可以发现，同一列的三个分布都非常的相似。这说明，足够的采样是可以逼近真实概率分布的；也说明他们的方法可以很好的将图拓扑结构展现出来。

 

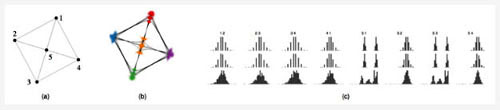
图9 (a)期望图；(b)根据文章的方法得到的布局；(c)边的统计信息分布图

在第二个例子中，他们尝试用这个方法分析城市之间的行程时间。该例子分析了8个城市之间的行程时间。在构图上，他们将每个城市看作顶点，在可到达的城市之间建立边。边的权重表示行程时间。为获取城市之间的行程时间，他们通过Google Direction API随机获取不同时间段，任意两个连接的城市之间的行程时间，并通过直方图处理，获取城市之间行程时间的概率分布图(如图10(a)所示)。

接着，他们根据不同的参考布局，得到了不同的概率图布局。图10(b)和(c)展示的布局，在其参考布局中，顶点的位置是不确定的，但顶点之间的理想距离是相应城市之间的真实距离。图10(d)和(e)展示的布局，在其参考布局中，顶点的位置就是相应城市的地理位置。我们可以发现，这两类参考布局得到的最后布局非常的相似，它们似乎只是旋转了不同的角度。

 

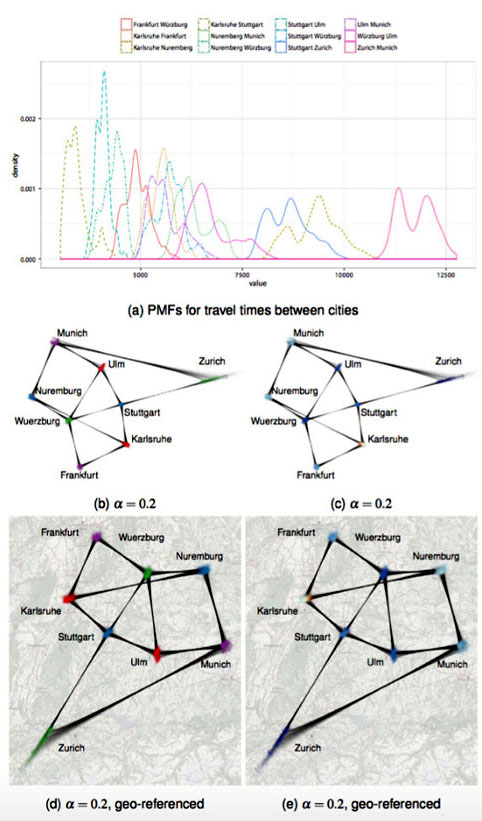
图10 (a)城市之间行程时间的概率分布图；(b)(c)和(d)(e)是两种参考布局得到的概率图布局

总的来说，这篇文章提出了一个新颖的不确定网络的可视化方法。他们的方法可以清晰的展现图的拓扑结构和图中不确定信息的概率分布。

(责任编辑：安博涛)