不确定网络,在本文表示顶点是确定的(certain),边的存在与否满足某种概率分布的网络。在图1中,左图是确定网络(certain graph),右图是不确定网络(uncertain graph)。
在不确定网络可视分析中,现有的方法往往直接在确定图(exact graph)中用视觉变量(visual variables)表示不确定信息。这些方法可以很好的将图的拓扑结构展示出来,但忽略了不确定信息的概率分布情况。
在这篇文章[1],作者们提出一个概率图(probabilistic graph)布局方法。这个方法可以同时展示图的拓扑结构和不确定信息的概率分布。它的基本思想是,依据蒙特卡洛方法(Monte Carlo process)对不确定图进行采样;将采样获得图根据力导向算法进行布局;之后,将所有采样图的力导向布局组合起来,获得最后概率图的布局(如图2所示)。
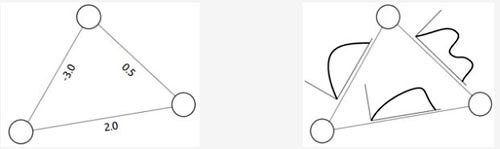
图1 左图是确定图;右图是不确定图
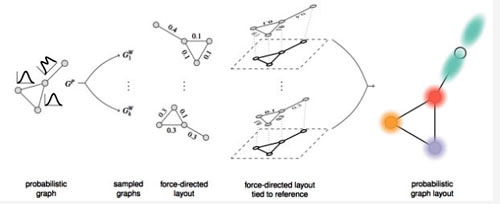
图2 文章提出的概率图布局方法流程图
文章分析的数据可以用G = (V, E, F)表示,其中V表示顶点集合。顶点是确定的元素;E表示边集合。边的存在与否满足F表示的概率密度函数。
在采样阶段,采用随机采样方法。
在力导向布局阶段,他们采用图3公式优化图布局。其中dij表示顶点i和顶点j之间的理想距离;wij表示边被选取的概率。
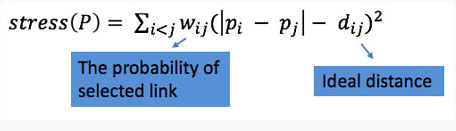
图3 力导向算法优化函数
在组合阶段,目标是将所有采样图的力导向布局整合成一个布局。文章提出的方法是构建一个参考布局(reference layout),然后将所有的采样图根据图4公式,重新布局。

图4 根据参考布局,重新布局的优化函数
在文中,参考布局一般是期望图(expected graph)。在期望图中,边的权重是该边概率分布的期望值。
在可视化阶段,为了更好的将每个顶点的位置分布情况和整体的图结构展示出来,他们对最后计算得到的整合布局进行了一系列的处理。
首先,他们对图中的顶点进行了滚雪球(splatting)处理。这样处理的目的是为了更好的将相同顶点的可能位置展示出来。在实际处理中,他们采用核密度估计函数计算每个顶点位置的概率密度分布函数,然后用ray-casting的方法,将顶点的位置分布展现出来(图5)。在核密度估计函数中,带宽h的值对结果的影响很大。图6展示了在不同h的情况,获取的结果。从左至右,布局从欠平滑状态过渡到过平滑状态。文章作者认为欠平滑的布局更利于用户进一步的分析,因为欠平滑的布局可以清晰展现顶点和边的关系。
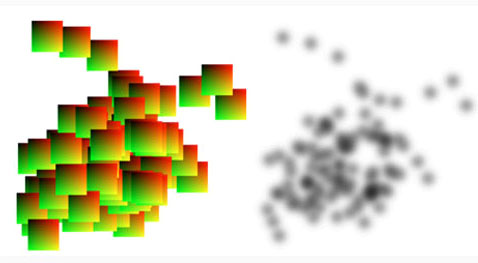
图5
左图每个方块表示每个顶点位置的概率密度分布;右图是在左图基础上进行ray-casting后得到的布局

图6 从左至右,布局从欠平滑状态过渡到过平滑状态
(责任编辑:安博涛)