1960年,尤金·维格纳在《数学在自然科学中不合理的有效性》中论证了数学概念和发现的非比寻常的能力。通常,那些概念和发现仅仅只是数学家为了追求其内在结构和美而发展出来的,但在后来却成为了描述物理世界的强有力工具。2017年的阿贝尔得主Yves Meyer(伊夫·梅尔)是将对纯数学研究带到现实世界中的实际应用的典范。(阿贝尔奖是数学界的最高荣誉之一,2016年获得该殊荣的就是证明了困扰数学家300多年的费马大定律的安德鲁·怀尔斯。)
△ Yves Meyer与小波。(图片来源:Olena Shmahalo/Quanta Magazine)
今年的阿贝尔奖授予Yves Meyer,以表彰他在小波理论的发展中所发挥的重大作用。小波理论允许我们将各种不同类型的信息分解为更简单的组件,从而使信息分析、处理和储存变得更加简单。因此,小波理论被应用在非常广泛的领域中,包括调和分析应用和计算、数据压缩、降噪、医学成像、归档、数字电影以及引力波探测等等。
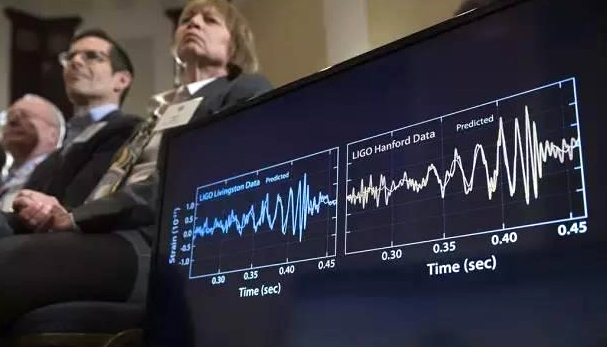
△ 2016年,LIGO探测到两个黑洞合并辐射出的引力波事件,其信号分析正是应用了小波理论。(图片来源:Shawn Thew /Epa/REX/Shutterstock)
有趣的是,Meyer的工作灵感并不是来自于数学的,而是来自于石油工业。在1980年代,法国工程师Jean Morlet想要知道如何更好的利用地震数据来寻找石油。Morlet分析了从石油勘探中收集到的反射数据。将振动向地面传送,并收集回声。这跟蝙蝠利用声呐的原理一样。问题是如何分析反射回来的数据,并提取关于石油层的有价值的信息。Morlet和物理学家Alex Grossmann想到了一个分析信号的方法,并且引入了一种新的函数类别,称为“小波”(wavelets),该函数通过对固定函数进行伸缩和平移而得出。然而,石油工业对此并不感兴趣。Morlet的方法并没有被采用,但他们的论文依然在1984年的春天发表在科学期刊上。
一年之后,Meyer正在巴黎综合理工学院复印东西的时候,他的同事给他复印了关于Morlet的那篇论文。在前往马赛的火车上,他发现了小波的巨大潜力。
数学家和工程师早就知道一个分析和处理特定类型信息的强大工具:傅里叶分析。声音是用来解释傅里叶分析的最佳例子。例如,音叉发出来的中央A的声音由一个完美的正弦波代表,就比如下面这个:

△ 这是一个正弦波。它往左和右无限地延伸。由于正弦波和余弦波相关,因此这也可以看做是余弦波的表示。(图片来源:Plus)
其它的声音,比如小提琴奏出的相同音符,就更加复杂。但是,后来我们发现任何周期性的声音,事实上是任何类型的周期信号,都可以被分解成不同频率的正弦波和余弦波的总和。

△ 函数 f 会随着时间改变,代表了一个声波。傅里叶变换过程会将函数f分解成特定频率和振幅的正弦波。傅里叶变换被表示为频域上的峰值,峰值的高度显示了那个频率下的波的振幅。(图片来源:Wikipedia)
傅里叶分析是个非常有用的工具。它也可以被用来分析和处理图像以及其它类型的信息。但是,它也有缺陷:因为基本的组件——正弦波和余弦波——是周期性的,傅里叶分析只有在重复信号中才能发挥最强大的作用。但对于那些具有不规则特征(比如峰值等)的非周期信号就不是那么管用了。不幸的是,在大部分现实生活的现象中,从说话的声音到地震数据,都属于非周期类别。
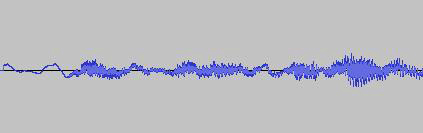
△ 这个波形来自人类的声音。它有规律,但不是周期的。(图片来源:Plus)
(责任编辑:安博涛)